Naar aanleiding van mijn vorige column over een short strangle op TomTom is er een levendige discussie ontstaan of het verkopen van een put gelijk is aan het kopen van een aandeel in combinatie met het verkopen van een call. In deze column zal ik dieper ingaan op dit blijkbaar gevoelige onderwerp.
Het schijnt dat in verschillende boeken over beleggen / opties staat dat een short put altijd gelijk is aan een short call tezamen met het onderliggende aandeel. Nu is het zo dat als iets op papier staat het niet per definitie wil zeggen dat iets ook daadwerkelijk waar is. Maar uit ervaring weet ik dat zeer veel theorieboeken met grote zorg zijn geschreven en dat je het dus niet zo maar terzijde kunt schuiven.
Put–call pariteit
Op maar meteen met de deur in huis te vallen, een short put en een aandeel in combinatie met een short call lijken zeer veel op elkaar. Immers, in beide gevallen koop je onderliggend een aandeel. Daarnaast leert de put-call pariteit ons dat er een verband tussen beide is. De put-call pariteit is de relatie tussen de premie van een call optie en de premie van een put optie met dezelfde looptijd en uitoefenprijs. Deze relatie geldt alleen voor opties Europese stijl en is gebaseerd op de formule:
P + S = C + CW (X)
hetgeen betekent dat de waarde van een call (C) gelijk is aan de waarde van een aandeel (S) plus de waarde van een put (P) min geldbedrag ter hoogte van de contante waarde van de uitoefenprijs. Mocht het aandeel dividend betalen dat moeten we de CW (X) verhogen met de contante waarde van het dividend. Concreet betekent dit bijvoorbeeld dat je een call optie met uitoefenprijs 100,00 en een looptijd van vijf maanden op een aandeel (koers 99,00) kunt nabootsen door het aandeel en een put met gelijke uitoefenprijs en looptijd te kopen en deze investering (grotendeels) te bekostigen door een lening ter grootte van de contante waarde van 100,00. Indien de vijfmaands rente 3 % bedraagt, het verwachte dividend gedurende de looptijd van de opties 1,50 is en de vijfmaands put 100,00 noteert 4,00, dan is de call premie als volgt te berekenen: 99,00 + 4,00 – 1,48 – 98,77 = 2,71.
Deze put-call pariteit betekent echter niet dat een aandeel met short call altijd gelijk is aan een short put. Sterker nog, hoewel ze op elkaar lijken zullen ze vaker net iets verschillen dan dat ze hetzelfde zijn. Het verschil heeft te maken met de gekozen uitoefenprijzen.
Hieronder zal ik twee voorbeelden behandelen om één en ander te verduidelijken. Het eerste voorbeeld is de constructie op TTM van mijn vorige column. Daarna behandel ik een voorbeeld waarbij ik zeer uiteenlopende uitoefenprijzen kies.
Voorbeeld 1
| Koop aandeel TTM | 6,25 |
| Verkoop call TTM dec 2011 strike € 6,40 | 0,95 – |
| Verkoop put TTM dec 2011 strike € 5,60 | 0,60 – |
| Investering | € 4,70 |
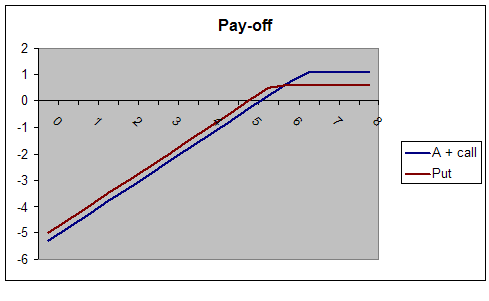
Om te kijken of het aandeel met short put gelijk is aan de short call, heb ik hieronder de pay-off grafieken van beide weergegeven. Waar het uiteindelijk om gaat is wat het break-even punt is, het maximale verlies en uiteraard de maximale winst.
Uit bovenstaande grafieken blijkt dat het aandeel met short call een hogere maximale winst heeft, maar tevens een groter maximaal verlies. Ook ligt het break-even punt anders. Bij het aandeel met call is de maximale winst € 1,10, het maximale verlies € 5,30 en het break-even punt ligt op € 5,30. Bij de short put is de maximale winst € 0,60, het maximale verlies € 5,00 en het break-even punt ligt hiermee dus ook op € 5,00.
Voorbeeld 2
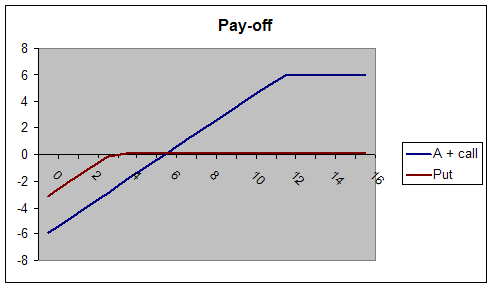
Bij het onderstaande voorbeeld heb ik wat gekke uitoefenprijzen gekozen om het verschil tussen beide combinaties duidelijk te maken. Tevens zijn de prijzen gebaseerd op de slotkoersen van vrijdag. Ik koop het aandeel op € 5,96 en verkoop de call dec 2011 met uitoefenprijs 12 voor € 0,06 en verkoop de put dec 2011 met uitoefenprijs € 3,20 voor € 0,07. Hieronder vindt u wederom de pay-off grafieken. Vanwege de extreme uitoefenprijzen blijken de verschillen pas goed. De reden is eigenlijk vrij simpel. Beide opties zijn zwaar out-of-the money waardoor je bij het aandeel met short call eigenlijk alleen het aandeel hebt en bij de short put feitelijk nauwelijks een aandeel koopt.
Bij het aandeel met call is de maximale winst € 6,00, het maximale verlies € 5,90 en het break-even punt ligt op € 5,90. Bij de short put is de maximale winst € 0,07, het maximale verlies € 3,13 en het break-even punt ligt hiermee dus ook op € 3,13.
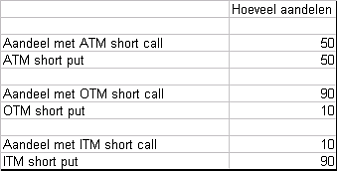
Als belegger moet je dus vooral kijken wat je deltapositie is. Of anders gezegd, hoeveel aandelen koop ik nu. Als particuliere belegger is het wellicht lastig om achter de exacte delta positie te komen. Deze is wat mij betreft ook niet nodig, maar je moet wel een globaal beeld van je positie hebben. De tabel hieronder kunt u als hulpmiddel beschouwen. De OTM en ITM zijn zeer extreem en kennen in onderstaande tabel dan ook (haast) geen delta.
Overige verschillen
Om volledig te zijn, wil ik vermelden dat er ook nog andere verschillen zijn die niet direct zichtbaar zijn in de grafieken. Het eerste is natuurlijk dat de short put een marginverplichting oplevert. Maar hier staat de lagere investering tegenover (sterker nog, er is bij het aangaan van de transactie geen investering). Daarnaast levert een aandeel wellicht dividend op en een short put niet. Voor de pay-off grafieken levert dit niet een wezenlijke verandering op omdat het verwachte dividend verwerkt zit in de koers van de call en de put. Mocht het dividend echter wijzigen dan zal dit wel degelijk gevolgen hebben voor het rendementsverschil.
Rente
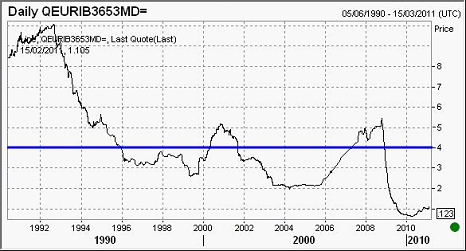
Optieprijzen worden ook beïnvloed door de rentestand. Bij een lage rente zijn calls relatief goedkoop en puts relatief duur. Immers de verkoper van een put moet contanten aanhouden ter dekking van zijn koopplicht. Op die contanten krijgt hij een lage rente. Om toch een aantrekkelijk rendement te behalen, zal hij gecompenseerd willen worden door een hogere putpremie. Bij calls werkt dit andersom: de verkoper van een call moet de onderliggende aandelen aanhouden om te kunnen voldoen aan zijn leveringsplicht. Hij derft slechts een lage rente terwijl hij recht houdt op het dividend.
Op dit moment is de rente erg laag en het is niet onwaarschijnlijk dat de rente in de toekomst weer eens gaat stijgen.
Voor de verkoper van de call is een stijgende rente dus uiterst nadelig. Tevens zal een rentestijging ceteris paribus ook tot een daling van het aandeel leiden. De verkoper van de put daarentegen is goed uit.
Kortom, in hoofdlijnen lijken beide optiestrategieën op elkaar, maar de maximale winst/verlies zal volledig afhangen van de onderliggende deltapositie.
drs Richard H.J. de Jong RBA is adjunct directeur vermogensbeheer bij Van Lieshout & Partners N.V.
Persoonlijke noot: Ik wil de verpleegsters van de kinderafdeling in Leiden en vooral de hartchirurg en alle andere mensen van de kinder OK uit de grond van mijn hart bedanken voor al hun geweldig werk en goede zorgen.

5 gedachten over “Short put = Aandeel met short call ?”
Ik stel vast dat je mijn vorig bericht niet of maar met één oog gelezen hebt. Je maakt namelijk exact dezelfde fout.
Nogmaals: “aandeel + verkocht call = verkochte put met dezelfde strike als de call”.
Concreet:
-Je koopt vandaag Tomtom aan een koers van 5.9 euro en verkoopt de call 6.4 december 2011 voor 0.60 euro.
=> maximale winst: 1.1 euro / maximaal verlies: 5.3 euro
– Je verkoopt de put met strike 6.4 december 2011 voor 1.1 euro
=> maximale winst: 1.1 euro / maximaal verlies: 5.3 euro
Ik hoop dat het nu duidelijk is?
Mvg
Een covered call geeft wel degelijk hetzelfde pay-off schema als een short put. Uiteraard kan je voorbeelden aanhalen met optieprijzen waarbij de pay-off curve er lichtjes anders uit gaat zien dan bij een short put, door een verschil in de optieprijzen, maar theoretisch gezien komt de pay-off curve op hetzelfde neer.
Bij een short put heb je minder transactiekosten dan bij een covered call, dus een short put zou (ceteris paribus) een betere optiestrategie zijn.
Daar heeft de put-call pariteit (noch de delta van de strategie, noch de risicovrije rente, noch het dividend) iets mee te maken.
Zie ook:
Ken Fisher – The only 3 questions that count
Jack Schwager – The New Market Wizards
George Fontanills – The Options Course
Beste Kim,
In mijn stukje over put-call pariteit schrijf ik letterlijk: “call optie met uitoefenprijs 100,00 en een looptijd van vijf maanden op een aandeel (koers 99,00) kunt nabootsen door het aandeel en een put met gelijke uitoefenprijs en looptijd te kopen en deze investering (grotendeels) te bekostigen door een lening ter grootte van de contante waarde van 100,00”.
Dit is dus exact hetzelfde als jij schrijft !!!!!!!!!!! Waarom dat een fout is, is mij een compleet raadsel.
Echter, ik schrijf daaronder dat aandeel plus short call niet altijd gelijk is aan een put (namelijk als de uitoefenprijzen verschillen, of anders gezegd als de delta verschilt. Wederom weer exact hetzelfde als jij schrijft). Dit om alles voor elke lezer hopelijk duidelijk te maken.
Ik kan niet nog duidelijker zijn: ik ben het volledig eens met je stelling aandeel + verkocht call = verkochte put met dezelfde strike als de call. Alleen geef ik vervolgens daarna twee voorbeelden waarin de strikes niet gelijk zijn zodat mensen kunnen zien dat dit verband alleen opgaat bij gelijke uitoefenprijzen.
Ik probeer altijd elke reactie goed te lezen, hoewel ik ongetwijfeld soms zaken verkeerd interpreteer. Helaas kom ik er soms niet aan toe om te reageren. Probeer jij dan in het vervolg ook de columns goed te lezen ?
Dan is het me een raadsel waarom je deze column schrijft ter ‘verduidelijking’ van de commotie rond je vorig artikel.
Ik heb op je vorig artikel net hetzelfde geschreven als wat ik nu schrijf. Je antwoordde toen dat ik het fout had en dat beide niet gelijk zijn. Als jij dan ook mijn bericht goed gelezen zou hebben, waarom dan het bericht dat ik fout was? Uiteraard moeten de uitoefenprijzen gelijk zijn, maar dat is de evidentie zelve. Ik heb dat trouwens ook aangegeven in een volgend bericht op die pagina.
Ik vroeg je toen waarom je niet gewoon twee put opties schrijft als je dit transactiekosten bespaart.
Aangezien het nogal vermoeiend wordt, mijn laatste reactie. Kim, de vorige keer schreef je: Voor deze strategie kan je toch ook gewoon twee puts schrijven… Dit is dan exact dezelfde strategie alleen betaal je minder transactiekosten”.
Ik heb nu laten zien dat dat niet zo is (zie max. winst etc). Zoals jij ook later zeer terecht opmerkt zijn beide echter wel aan elkaar gelijk als de uitoefenprijzen aan elkaar gelijk zijn, maar anders dus vaak niet. Maar ik denk dat je in je allereerste bedoelde: Voor deze strategie kun je ook gewoon twee puts schrijven met dezelfde uitoefenprijs als de call !!!!!!!!! Dan hadden we geen discussie gehad. Die toevoeging is echt van belang, zoals ik heb laten zien.
Voor de goede orde, dit schrijf je inderdaad in een latere reactie, maar ik kan natuurlijk niet aan de gang blijven.
Maar dan nu een antwoord op je echte vraag: Ik heb in mijn voorbeeld niet gekozen voor twee puts met dezelfde strike als de call (dus 6,40), omdat ik in mijn voorbeeld een iets lagere putstrike wilde. Dus geen put 6,40, dat vond ik net te agressief.
Uiteraard had ik best twee puts op 5,6 kunnen geven, maar dit leidt gegeven mij positieve visie tot een iets slechtere pay off. De maximale winst scheelt € 0,50. De extra transactiekosten doen dat echt niet teniet. (Althans dat hoop ik want anders is je broker wel een beetje duur)
Volgens mij zijn we er zo helemaal uit.